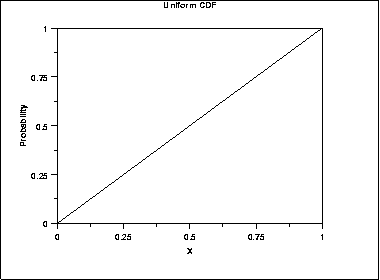
Cdf of Uniform Distribution

By Coa_295Zack 26 Aug, 2022 Post a Comment

The mean of the uniform distribution is μ 1 2 a b. For example to use the normal distribution include coderConstantNormal in the -args value of codegen MATLAB Coder.

The Cumulative Distribution Function For The Continuous Uniform Distribution Youtube

Wilcoxonank Sum Statistic Distribution in R.

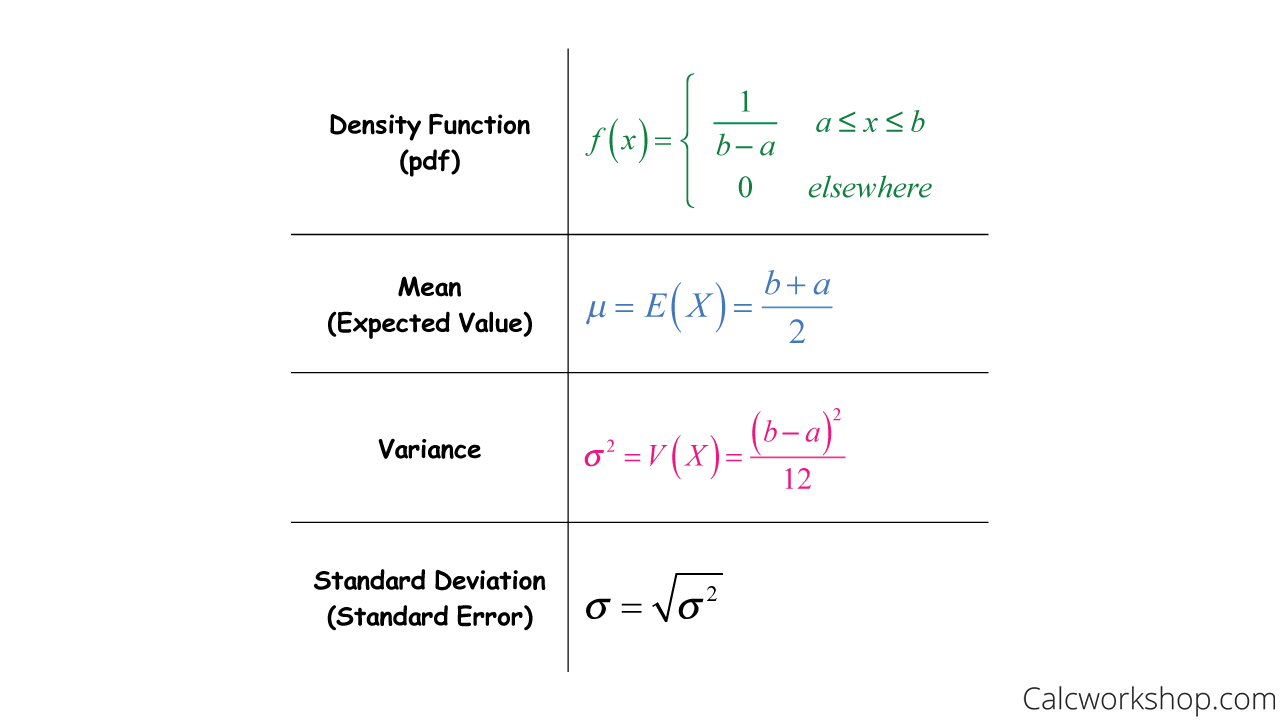
. In probability theory and statistics the hypergeometric distribution is a discrete probability distribution that describes the probability of successes random draws for which the object drawn has a specified feature in draws without replacement from a finite population of size that contains exactly objects with that feature wherein each draw is either a success or a failure. Know as a cumulative distribution function CDF which is a function from the sample space Sto the interval 01 ie F. CDF of Log Normal Distribution.

A in the formula is the minimum value in the distribution and b is the. The standard arcsine distribution is a special case of the beta distribution with α β 12. In probability theory and statistics the discrete uniform distribution is a symmetric probability distribution wherein a finite number of values are equally likely to be observed.

Weibull Distribution in R. The input argument name must be a compile-time constant. In general the CDF can take any form as long as it de nes a valid probability statement such that.

For 0 x 1 and whose probability density function is on 0 1. In probability theory the arcsine distribution is the probability distribution whose cumulative distribution function involves the arcsine and the square root. It converges with probability 1 to that underlying distribution.

For any measurable set. In particular by solving the equation we get that. In the standard form the distribution is uniform on 0 1Using the parameters loc and scale one obtains the uniform distribution on loc loc scale.

Any two probability distributions whose moments are identical will have identical cumulants as well and vice versa. 522 Joint Cumulative Distribution Function CDF We have already seen the joint CDF for discrete random variables. The input argument pd can be a fitted probability distribution object for beta exponential extreme value lognormal normal and Weibull distributions.

In probability and statistics the IrwinHall distribution named after Joseph Oscar Irwin and Philip Hall is a probability distribution for a random variable defined as the sum of a number of independent random variables each having a uniform distribution. It is not possible to define a density with reference to an. The first cumulant is the mean the second cumulant is the variance and the third cumulant.

The joint CDF has the same definition for continuous random variables. The inverse of the cdf can be used to translate results obtained for the uniform distribution to other distributions. The mode is the point of global maximum of the probability density function.

If u is a uniform random number on 01 then x F-1 u generates a random number x from any continuous distribution with the specified cdf F. In probability and statistics the logarithmic distribution also known as the logarithmic series distribution or the log-series distribution is a discrete probability distribution derived from the Maclaurin series expansion. The variables in a uniform distribution are called uniform random variables.

The empirical distribution function is an estimate of the cumulative distribution function that generated the points in the sample. Given a uniform distribution on 0 b with unknown b the minimum-variance unbiased estimator UMVUE for the maximum is given by where m is the sample maximum and k is the sample size sampling without replacement though this distinction almost surely makes no difference for a continuous distributionThis follows for the same reasons as estimation for. From this we obtain the identity This leads directly to the probability mass function of a Logp-distributed random variable.

Uniform distribution ecology Equidistributed sequence. More precisely the probability that a normal deviate lies in the range between and. In addition to the video I can recommend to read the other articles on my website.

For an example see Compute Continuous Uniform Distribution cdf. The cumulative distribution function CDF or cdf of the random variable X has the following definition. The mean of a uniform random variable X is.

All pages with titles containing uniform distribution. The expected value ie. The variance of the uniform distribution is σ 2 1 12 b.

The result p is the probability that a single observation from a uniform distribution with parameters a and b falls in the interval a x. Uniform distribution may refer to. For any given x2S the CDF returns the probability Fx PX x which uniquely de nes the distribution of X.

Uniform Distribution in R. Frequently seen patterns include the normal distribution uniform distribution binomial distribution etc. And about 997 are within three standard deviations.

The inversion method relies on the principle that continuous cumulative distribution functions cdfs range uniformly over the open interval 01. EX b a 2. Methods of sampling a non-uniform distribution are typically based on the availability of a pseudo-random number generator producing numbers X that are.

Pseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution. EX 12 a b This is also written equivalently as. Wilcoxon Signedank Statistic Distribution in R.

Since the log-transformed variable has a normal distribution and quantiles are preserved under monotonic transformations the quantiles of are where is the quantile of the standard normal distribution. Expected Value and Variance. About 68 of values drawn from a normal distribution are within one standard deviation σ away from the mean.

In the continuous univariate case above the reference measure is the Lebesgue measureThe probability mass function of a discrete random variable is the density with respect to the counting measure over the sample space usually the set of integers or some subset thereof. The cdf is not discussed in detail until section 24 but I feel that introducing it earlier is better. Every one of n values has equal probability 1nAnother way of saying discrete uniform distribution would be a known finite number of outcomes equally likely to happen.

Uniform source A uniform continuous random variable. About 95 of the values lie within two standard deviations. For this reason it is also known as the uniform sum distribution.

The cumulative distribution function CDF of a probability distribution contains the probabilities that a random variable X is less than or equal to X. F_XtPXle t The cdf is discussed in the text as well as in the notes but I wanted to point out a few things about this function. In probability theory and statistics the cumulants κ n of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution.

Log Normal Quantile Function qlnorm Function. This fact is known as the 68-95-997 empirical rule or the 3-sigma rule. International Encyclopedia of Education Third Edition 2010.

The cumulative distribution function CDF of 2 is the probability that the next roll will take a value less than or equal to 2 and is equal to 3333 as there are two possible ways to get a 2 or below. The generation of pseudo-random numbers having. Python for Data Science.

On the other hand the. Conversely if U is. Generate random numbers from the Weibull.

As an instance of the rv_continuous class uniform object inherits from it a.

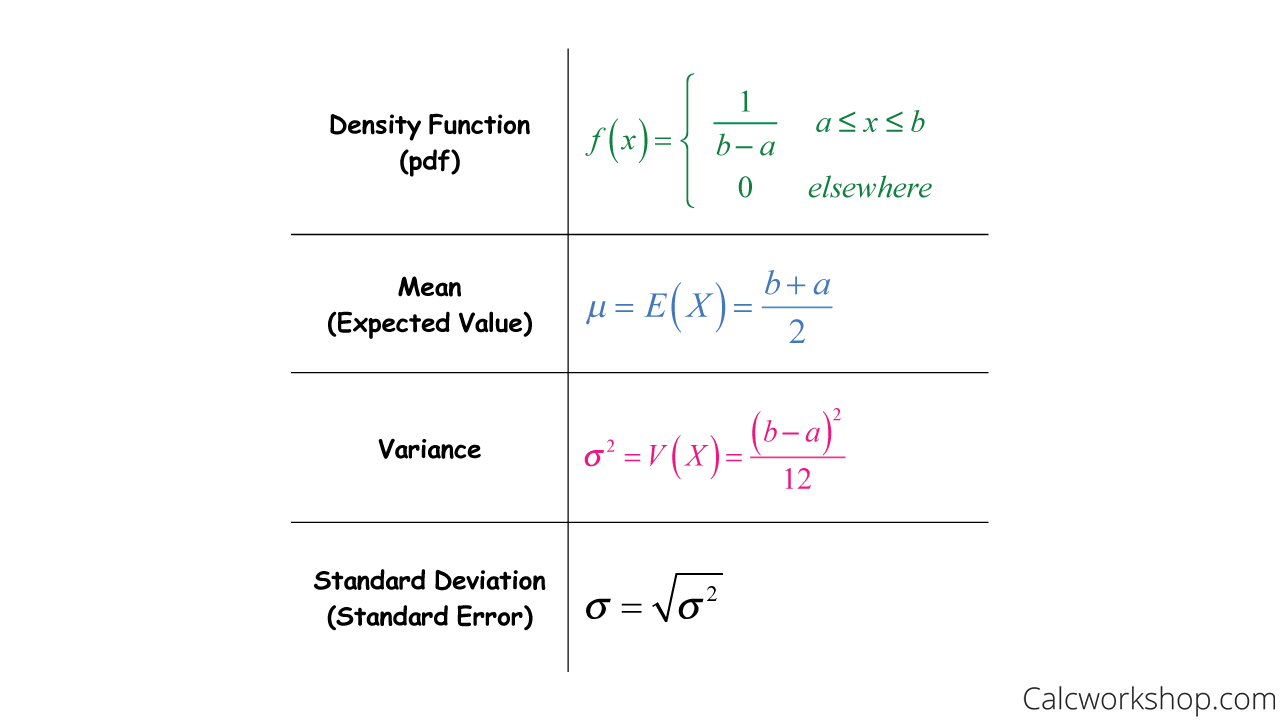
Continuous Uniform Distribution Defined W 5 Examples

Solved Specific Forms Of The Pdf Cdf Distribution Mean Chegg Com